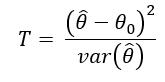| Elies Furió Blasco | Matilde Alonso Pérez |
| elies.furio-blasco@univ-lyon3.fr | matilde.alonso@univ-lyon2.fr |
| Universidad de Lyon | Universidad de Lyon |
Resumen: La prueba de Wald es un contraste de hipótesis donde se trata de ver la coherencia de afirmar un valor concreto de un parámetro de un modelo. Se presentan las principales características y limitaciones de la prueba de Wald.
Résumé : Le test de Wald est un test d’hypothèse qui permet de vérifier la cohérence de l’affirmation d’une valeur particulière d’un paramètre d’un modèle. Cette note présente les principales caractéristiques et limites du test de Wald.
Abstract: The Wald test is a hypothesis test where the consistency of asserting a particular value of a parameter of a model is tested. This note presents the main features and limitations of the Wald test.
Índice
2.1 Utilización de la prueba de Wald
2.2 Limitaciones de la prueba de Wald
2.3 Aplicación del test de Wald
Abraham Wald
Abraham Wald fue un matemático húngaro nacido en 1902. Se graduó y realizó la tesis doctoral en Viena bajo la dirección de Karl Menger. Fue investigador de la Universidad de Columbia y formó parte de la Comisión Cowles de Investigación en Economía de dicha universidad.
En un principio, se interesó en la teoría de conjunto y la geometría. Posteriormente, desarrollo contribuciones interesantes en el ámbito de la teoría de la decisión, la econometría y el análisis secuencial. Durante el periodo 1933-39, publicó diferentes contribuciones en dichos ámbitos[1]. Posteriormente, publicó artículos y libros relativos al análisis secuencial e inspección de muestreo[2] [3] [4]. En el ámbito de la Economía, publico una propuesta de índice del costo de la vida[5]. Una relación de sus trabajos fue recogida por The Annals of Mathematical Statistics[6].
La prueba de Wald
La prueba de Wald es una prueba estadística paramétrica nombrada así en honor del estadístico Abraham Wald. Cada vez que hay una relación dentro o entre los datos se puede expresar un modelo estadístico con los parámetros a ser estimados a partir de una muestra. La prueba de Wald se utiliza para poner a prueba el verdadero valor del parámetro basado en la estimación de la muestra.
El Test de Wald es un contraste de hipótesis donde se trata de ver la coherencia de afirmar un valor concreto de un parámetro de un modelo probabilístico una vez tenemos ya un modelo previamente seleccionado y ajustado.
Se aplica siempre tras elegir un modelo (una distribución cualquiera, una regresión simple, una regresión logística, etc) y a continuación se hace algún contraste de hipótesis sobre uno o varios parámetros: Por ejemplo, la media de la normal es 5, la pendiente de la recta es 0, el coeficiente principal de una regresión logística es 0, etc.
En la prueba estadística Wald, la estima de máxima verosimilitud ô del parámetro(s) de interés θ se compara con el valor propuesto θ0, bajo la suposición de que la diferencia tipificada entre ambos seguirá aproximadamente una distribución normal. Típicamente, el cuadrado de la diferencia se compara con una distribución de chi-cuadrado. En el caso univariante, el Wald estadística es
Donde
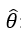
- : estimaciones de los parámetros
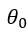
- son los valores de los parámetros propuestos, el bajo del parámetro bajo la hipótesis nula.
- El numerador es la diferencia entre el estimador y el valor bajo la hipótesis nula.
- El denominador es el error estándar del estimador.
En buena medida, se corresponde a una valoración de la distancia entre Observado y Esperado y se pretende valorar, en un contraste de hipótesis, si lo que obtenemos es o no muy distante de lo que esperamos, en el caso de ser cierta la hipótesis nula.
Para realizar una prueba de Wald, se siguen estos pasos generales:
- Formular la hipótesis nula (H0) y la hipótesis alternativa (H1).
- Calcular el estimador del parámetro () y su error estándar
- Calcular la estadística de prueba de Wald usando la Expresión 1.
- Comparar la estadística de prueba con los valores críticos de la distribución chi-cuadrado para determinar la significancia estadística.
Este estadístico sigue una distribución chi-cuadrado bajo la hipótesis nula. Se compara el valor calculado de T con los valores críticos de la distribución chi-cuadrado para determinar la significancia estadística.
Utilización de la prueba de Wald
La prueba de Wald se utiliza comúnmente en el contexto de modelos de regresión, pero la idea subyacente puede aplicarse en otras situaciones dónde se estime un parámetro y se desee probar su significancia.
Para realizar una prueba de Wald, sigue estos pasos generales:
- Formula la hipótesis nula (H0) y la hipótesis alternativa (H1).
- Calcula el estimador del parámetro () y su error estándar
- Calcula la estadística de prueba de Wald usando la Expresión 1.
- Compara la estadística de prueba con los valores críticos de la distribución chi-cuadrado para determinar la significancia estadística.
Se utiliza para contrastar si es cero o no un determinado coeficiente que multiplica a una variable independiente en una regresión.
- Si el p-valor es menor que 0.05 (o menor que 0.001), se rechaza esa hipótesis nula que afirma que ese coeficiente es cero, y se entiende entonces que ese coeficiente no es cero y que, por lo tanto, el modelo es útil para representar una determinada relación.
- Si, por el contrario, el p-valor es mayor que 0.05 (o mayor que 0.001) eso significa que el valor del coeficiente podría ser perfectamente cero y estar viendo lo que vemos, por lo tanto, esa variable no influye a la hora de determinar la variable dependiente (o también denominada, a veces, variable respuesta) del modelo de regresión.
Limitaciones de la prueba de Wald
A la hora de interpretar los resultados de la prueba de Wald, conviene tener presente una serie de consideraciones relativas a las posibles limitaciones de dicha prueba:
- Linealidad del modelo: la prueba de Wald se deriva asumiendo linealidad en el modelo. Si el modelo es no lineal, la prueba de Wald puede no ser la más apropiada, y podría ser preferible utilizar pruebas basadas en métodos de simulación o Bootstrap. Una aplicación del test de Wald en un modelo no lineal por medio de la simulación puede encontrarse en [7] y una corrección al test de Wald para la prueba de restricciones no lineales en [8].
- Dependencia de la muestra: La prueba de Wald puede ser sensible al tamaño de la muestra. En muestras pequeñas, la distribución de la estadística de prueba puede no seguir exactamente una distribución chi-cuadrado, lo que podría mermar la validez de las inferencias.
En muestras pequeñas, la prueba de Wald tiende a ser sesgada, y esto puede afectar la validez de las inferencias. En tales casos, pruebas basadas en métodos de remuestreo (como el bootstrap) pueden proporcionar resultados más robustos.
- Inestabilidad numérica: En algunos casos, especialmente cuando los estimadores son cercanos a los límites del espacio de parámetros, la prueba de Wald puede ser propensa a problemas de inestabilidad numérica.
Puede suceder que, al realizar largas cadenas de cómputos, los errores de redondeo pueden acumularse y que ocasionen una pérdida de validez de los resultados, dando lugar al fenómeno de inestabilidad numérica. Se dice que un proceso es inestable cuando los pequeños errores que se producen en una de sus etapas se agrandan en las etapas posteriores y se degrada seriamente la exactitud del cálculo en su conjunto.
En el análisis numérico, la estabilidad numérica es una propiedad de los algoritmos numéricos que describe cómo los errores en los datos de entrada se propagan a través del algoritmo. En un método estable, los errores debidos a las aproximaciones se atenúan a medida que la computación procede. La estabilidad numérica de un método junto con el número de condición define cuán buen resultado podemos obtener usando métodos aproximados para calcular cierto problema matemático. En un método inestable, cualquier error en el procesamiento se magnifica conforme el cálculo procede. Métodos inestables generan rápidamente anomalías y son inútiles para el procesamiento numérico.
- Asunciones de normalidad: La prueba de Wald se basa en la suposición de que los estimadores son asintóticamente normales bajo la hipótesis nula. Esta asunción puede no ser válida en todos los casos, especialmente en situaciones con sesgo o no normalidad.
- No robusta a violaciones de suposiciones: La prueba de Wald no es robusta frente a violaciones de algunas suposiciones clave, como la homocedasticidad de los errores y la independencia de los errores.
Una aplicación a la presencia de errores con una corrección de la prueba de Wald puede encontrarse en [9].
- Problemas con modelos ajustados mal: Si el modelo subyacente no se ajusta bien a los datos, la interpretación de la prueba de Wald puede ser cuestionable.
- Sensibilidad a valores atípicos: La presencia de valores atípicos puede afectar la validez de la prueba de Wald, especialmente en muestras pequeñas.
Estas limitaciones no han impedido un uso amplio de la prueba de Wald, especialmente porque su simplicidad y facilidad de cálculo, particularmente, en los casos de muestras grandes. No obstante, antes del uso de la prueba es sumamente conveniente revisar todas las circunstancias, así como valorar la oportunidad de llevar a cabo otras pruebas o métodos que, para el caso en cuestión, puedan mostrarse más apropiados.
Aplicación del test de Wald
seguir leyendo en Evaluación de parámetros. La prueba de Wald
Referencias
[1] O. Morgenstern, «Abraham Wald, 1902-1950», Econometrica, vol. 19, n.o 4, pp. 361-367, 1951, doi: 10.2307/1907462.
[2] A. Wald, «Sequential Tests of Statistical Hypotheses», Ann. Math. Stat., vol. 16, n.o 2, pp. 117-86, 1945.
[3] A. Wald, Sequential Analysis. Nueva York: John Wiley and Sons, 1947.
[4] A. Wald, «Contributions to the Theory os Statistical Estimation and Testing Hypotheses», Ann. Math. Stat., vol. 10, n.o 4, pp. 299-326, 1939.
[5] A. Wald, «A New Formula for the Index of Cost of Living», Econometrica, vol. 7, n.o 4, pp. 319-331, 1939, doi: 10.2307/1906982.
[6] «The Publications of Abraham Wald», Ann. Math. Stat., vol. 23, n.o 1, pp. 29-33, 1952.
[7] T. Wang y L. Wu, «Multivariate one-sided tests for nonlinear mixed-effects models», Can. J. Stat., vol. 41, n.o 3, pp. 453-465, sep. 2013, doi: 10.1002/cjs.11180.
[8] S. L. de Paula Ferrari y F. Cribari-Neto, «On the corrections to the Wald test of non-linear restrictions», Econ. Lett., vol. 42, n.o 4, pp. 321-326, ene. 1993, doi: 10.1016/0165-1765(93)90079-R.
[9] G. Y. Yi y Y. Yan, «Estimation and hypothesis testing with error-contaminated survival data under possibly misspecified measurement error models», Can. J. Stat., vol. 49, n.o 3, pp. 853-874, sep. 2021, doi: 10.1002/cjs.11594.
[10] J. Bouziotis, M. Arvanitakis, y J.-C. Preiser, «Indice de masse corporelle et mortalité des patients hospitalisés pour COVID-19», Nutr. Clin. Métabolisme, vol. 36, n.o 1, Supplement, pp. S18-S19, feb. 2022, doi: 10.1016/j.nupar.2021.12.034.